Состав ядра

 

Атомное ядро состоит из А нуклонов: Z положительно заряженных протонов и A – Z нейтронов с зарядом, равным нулю. В ядре действуют силы ядерного (сильного) взаимодействия, осуществляющие взаимное притяжение нуклонов и превышающие силы электростатического отталкивания протонов. Число А называется массовым числом атомного ядра, Z – атомным номером элемента. Изотопами называются атомы одного и того же химического элемента, обладающие разным числом нейтронов при одинаковом числе протонов (разные A – Z при одинаковом Z).

Масса нуклида в основном состоянии M(A,Z) является фундаментальной константой и складывается из массы ядра M(A,Z) и массы Z связанных в атоме электронов (при этом необходимо учитывать, что последняя составляющая много меньше первой). Массы нуклонов и нуклидов удобнее измерять в атомных единицах массы – а.е.м. (1 а.е.м. = 1/12 массы изотопа  ,или 931,5 МэВ, либо 1,66·10^-27 кг).

 

Энергия связи нуклонов в ядре. Эффект выделения энергии.

 

Массы ядер всегда меньше суммы масс составляющих их нуклонов, так как потенциальная энергия связанной системы (ядра) всегда меньше потенциальной энергии свободных нуклонов. Энергия, которую необходимо затратить, чтобы разделить ядро на составляющие его нуклоны, называется энергией связи ядра. Ее можно определить следующим образом:

                                                  Е_св = [Zm_p + (A – Z)m_n – M(A,Z)]c².                                             (1)

В таблицах, как правило, приводят значения масс нуклидов, поэтому удобнее использовать следующую запись (с точностью до энергии связи электронов):

                                         .                                     (2)

При использовании выражений (1) и (2) необходимо помнить, что энергия связи ядра на несколько порядков меньше полной энергии, соответствующей массе Е = Мс² из соотношения Эйнштейна (каждому значению массы М соответствует энергия Е), и для получения достаточно точного результата необходимо знать значения масс с точностью не менее шести знаков (при вычислении возникает небольшая разность).

Рассмотрим отношение энергии связи ядра к массовому числу

.

По определению ε есть средняя энергия связи, приходящаяся на один нуклон (удельная энергия связи нуклона в ядре). Тем самым она характеризует интенсивность ядерных сил. Как видно из рис. 1, при малых значениях массовых чисел ε резко возрастает и достигает максимума при А ≈ 5060 (порядка 8,38,8 МэВ). Нуклиды с такими массовыми числами наиболее устойчивы. С дальнейшим ростом А средняя энергия связи уменьшается, однако в широком интервале массовых чисел значение удельной энергии связи почти постоянно (=8 МэВ). Из сказанного следует, что можно записать

                                                                      .                                                                 (3)

Нетрудно понять, что если бы каждый нуклон ядра взаимодействовал с (А – 1) другими нуклонами, то полная энергия этого взаимодействия была бы пропорциональна произведению А(А – 1) ≈ А. Отличие этого соотношения от (3) указывает на свойство насыщения ядерных сил: каждый нуклон в ядре взаимодействует не со всеми остальными, а только с ограниченным числом соседних нуклонов. Ядерные силы – это силы притяжения, и, как свидетельствует факт существования стабильных ядер, при некоторых условиях они больше сил кулоновского отталкивания (энергия кулоновского отталкивания двух соседних протонов в ядре на порядок меньше энергии притяжения).

 

Зависимость средней энергии связи ε, отнесенной к одному нуклону, от массового числа

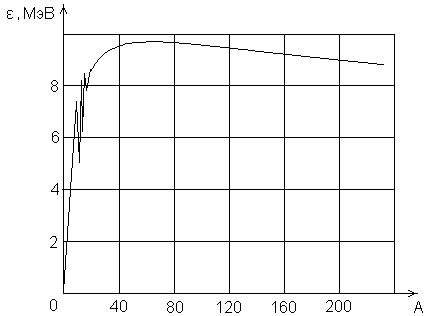
Рис.1

 

Высвобождение энергии в реакциях синтеза или деления ядер обусловлено увеличением ε в процессе слияния самых легких ядер в более тяжелые или в процессах деления тяжелых ядер. Локальные максимумы кривой ε (А) связаны с образованием устойчивых ядерных оболочек.

Форма зависимости энергии связи от массового числа привела к мысли об аналогии между ядром и каплей жидкости, что привело к созданию капельной модели ядра и получению полуэмпирической формулы Вайцзеккера для энергии связи ядра.

,

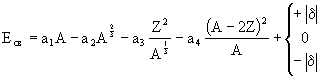где а₁ =  15,75 МэВ; а₂ = 17,8 МэВ; а₃ = 0,71 МэВ; а₄ = 23,7 МэВ; │δ│ = 34·А^-3/4. Первое слагаемое обуславливает пропорциональность энергии связи ядра и массы ядра равноценностью нуклонов ядра и взаимодействием каждого из них только с близлежащими соседями. Второе слагаемое учитывает то, что нуклоны на поверхности ядра взаимодействуют с меньшим числом других нуклонов и связаны с ними, таким образом, слабее (испарение молекул капли жидкости протекает с ее поверхности). Это приводит к уменьшению энергии связи ядра. Общее число «поверхностных» нуклонов пропорционально R² ~ А^2/3. Третье слагаемое учитывает наличие сил кулоновского отталкивания между протонами (ΔЕ_кул ~ Z(Z – 1)/R ≈ Z²/R ~ Z²/A^1/3). Четвертое слагаемое учитывает наличие протон-нейтронной асимметрии (наличие спина). Пятое слагаемое учитывает влияние четности Z и A – Z на устойчивость ядер: для четных-четных ядер (четное А и четное Z) подставляется в формулу +│δ│; для нечетно-нечетных ядер (четное А и нечетное Z) подставляется в формулу -│δ│; для нечетно-четных и четно-нечетных ядер (все остальные варианты) в формулу Вайцзеккера подставляется 0.

 

 

 

Энергия возбуждения составного ядра

 

По механизму взаимодействия ядерные реакции делятся на два вида: реакции с образованием составного ядра и прямые ядерные реакции (упругое потенциальное рассеивание). Согласно теории реакции с образованием составного ядра (разработана Н. Бором в 1936 году), реакция идет в два этапа. Сначала исходные частицы образуют промежуточное (составное) ядро за время τ_я (время, необходимое для того, чтобы нейтрон пересек ядро - τ_я ≈ 10^-2310^-21 с). Составное ядро всегда образуется в возбужденном состоянии, так как оно обладает избыточной энергией, привносимой нейтроном в виде энергии связи нейтрона в составном ядре ε_n, и части его кинетической энергии, равной суммарной кинетической энергии ядра-мишени и нейтрона в системе центра масс. В случае неподвижного ядра-мишени:

где Е* - энергия составного ядра; Е – кинетическая энергия нейтрона; m_n – масса нейтрона; М – масса ядра; Е’ – часть кинетической энергии нейтрона, отданная ядру-мишени.

На втором этапе энергия перераспределяется между нуклонами составного ядра, однако этот процесс весьма длительный. В итоге энергия может сконцентрироваться на одном нуклоне (или нескольких), находящихся вблизи границы ядра и этот нуклон (нуклоны) может покинуть ядро. Наряду с вылетом нуклонов, ядро может претерпеть и другой тип распада – испускание γ-кванта.

 

Деление тяжелых ядер тепловыми и быстрыми нейтронами

 

Деление ядер является одним из множества возможных процессов при взаимодействии нейтронов с ядрами, именно он лежит в основе работы любого ядерного реактора. Энергетически выгодно деление тяжелых ядер, однако последние делятся с крайне низкой вероятностью это означает, что существует энергетический барьер, препятствующий делению.

В ядерном реакторе происходит деление тяжелых нуклидов от до . Возможность деления конкретных ядер определяется кинетической энергией нейтрона, его энергией связи и энергией барьера деления.

Также необходимо заметить, что существуют делимые элементы (способны делиться только под воздействием нейтронов определенных энергий) и делящиеся (делятся под воздействием нейтронов любых энергий). К последним относятся ,  и . Из них в природе встречается только , остальные получаются искусственным путем:

При делении ядер, как правило, образуется два осколка деления с соотношением масс 2:3 (см. рис. 2). 80% энергии деления составляет кинетическая энергия осколков деления. Остальная часть распределяется между нейтронами, γ-квантами, β^- -частицами и антинейтрино. Соотношение между остальными составляющими энергии деления слабо зависит от делящегося ядра и от энергии нейтрона, вызывающего процесс деления.

Энергия осколков деления, мгновенных γ-квантов и нейтронов превращается в тепло практически мгновенно. Энергия β^- -распада (~ 7% всей энергии деления) выделяется постепенно в течение длительного промежутка времени, так как сами процессы β^- -распадов происходят с большими сдвигами во времени по отношению к моменту деления ядра. Это запаздывание приводит к существованию так называемого остаточного энерговыделения в остановленном ядерном реакторе.

Выход осколков деления

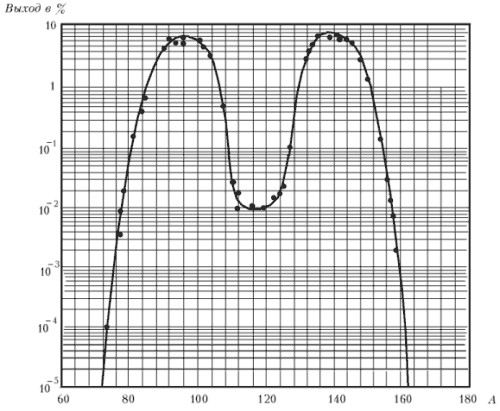
Рис.2